정확한 답이 필요하다면 float와 double는 피하라
우리가 흔히 쓰는 float와 double는 과학과 공학 계산용으로 설계되었다고 한다.
이진 부동소수점 연산에 쓰이고, 넓은 범위의 수를 빠르게 정밀한 근사치로 계산하도록 설계 되었다.
따라서 정확한 결과가 필요할 때 사용하면 안된다. 특히 금융 관련 계산에서는 float와 double 타입은 금융 관련 계산에는 맞지 않는다.
나는 사실 이번 아이템을 공부하기 전까지 이러한 부분에 대해 전혀 알지 못하고 있었다. float와 double은 실수를 사용하기 위한 자료형, 그리고 크기의 차이가 있다는 점 등등 만 생각하고 있었다.
그렇다면 왜 사용하면 안되는 지, 대안으로는 어떤 것이 있는 지 알아보자.
float와 double
float와 dobule은 부동 소수점 연산에 쓰인다고 했다. float와 double은 IEEE 754 부동 소수점 방식을 사용한다.
- 부동 소수점
- 숫자 아래와 같은 형태로 표현한다.
- value=(−1)sign×(1.fraction)×2^exponent
- Sign(부호 비트) : 숫자의 부호를 나타낸다.
- Exponent(지수) : 2의 몇 제곱인지를 나타낸다.
- Fraction(가수) : 실제 소수 부분을 나타낸다. 가수는 항상 1보다 크고 2보다 작은 숫자로 표현된다.
- IEEE 754 부동 소수점
- 부동 소수점 숫자를 32비트(float)와 64비트(double)로 표현하는 방식을 정의.
1
float f = 3.14f;
- 위 경우 부호 비트는 0 (양수)
- 지수: 128 + (지수 - 1) = 128 - (1) = 129 (1000 0001)
- 가수: 3.14를 이진수로 변환하여 저장
보다시피 이러한 부동 소수점 방식을 활용한 계산을 하게되면 실수를 표현할 때 정확한 표현이 아닌 근사치를 표현해 오차가 나타나게 된다. (0.1을 정확하게 표현하지 못한다.)
오차를 직접 확인해보자.
1
2
double value = 1.117;
double result = value - 0.32;
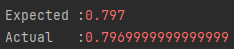
- 이 계산은 0.797을 예상할 것이다.
- 테스트를 해보면 위와 같이 근사값을 반환한다.
- 물론 어떤 계산은 정확하게 반환할 수 있지만, 0.1이나 0.2 등의 이진수로 정확히 표현할 수 없는 수가 나타난다면 위와 같이 미세한 오차가 발생하는 것이다.
- 이러한 오차는 금융 관련 계산에서는 치명적이다.
float와 double의 대안 (BigDecimal)
float와 double의 동작 방식을 알았고, 금융 관련 계산에서는 치명적이라는 사실도 알았다.
그렇다면 정확한 수치가 중요한 금융 계산 같은 경우에는 어떤 것을 사용해야 할까?
정수를 이용해 실수를 표현하는 BigDecimal이나 int, long을 사용하면 된다.
BigDecimal
Java에서 정수를 이용해 실수를 표현하는 BigDecimal을 제공한다.
1
2
3
4
5
6
public class BigDecimal extends Number implements Comparable<BigDecimal> {
private final BigInteger intVal;
private final int scale;
private transient int precision;
//...
}
- intVal
- 정수를 저장할 때 사용된다.
- scale
- 소수점 자릿수를 저장한다.
- precision
- 정밀도를 뜻한다. 수가 시작하는 위치부터 끝나는 위치까지의 총 자리수이다.
BigDecimal은 위와 같은 내부 변수들을 활용하여 실수를 정확하게 표현한다.
1
2
BigDecimal value = new BigDecimal("1.117");
BigDecimal result = value.subtract(new BigDecimal("0.32"));
- BigDecimal을 사용하면 어떤 실수를 넣더라도 정확한 값을 계산한다.
- 위에서 보다시피 객체를 생성한다. 반드시 문자열을 전달해야 하는 것은 아니지만, double 같은 타입을 전달할 경우 근사치가 전달되어 오차가 발생할 수 있다.
- 참고로 위와 같은 일반적인 생성자보다 valuOf 정적 팩토리 메서드가 권장된다.
- valueOf를 활용할 경우
캐싱된 값부터 탐색하거나 혹은 double의 경우toString을 통해 변환하여 생성하기 때문에 생성자를 통한 근사치를 신경쓰지 않아도 된다.
- valueOf를 활용할 경우
그러나 이렇게 정확한 BigDecimal에는 단점이 있다.
- 기본 타입보다 쓰기 훨씬 불편하고 느리다.
- 단발성 계산이라면 느린 문제는 무시할 수 있지만 쓰기 불편하다는 문제는 아쉽다.
BigDecimal 주의 사항
BigDecimal은 주의해야 할 사항이 하나 있다.
Comparable을 구현했기 때문에 객체간의 비교가 가능한데, BigDecimal은 규약 한 가지를 지키지 않고 있어 주의해야 한다. (아이템 14)
- x.compareTo(y) = 0 이면 x.equals(y) 여야 한다. 의 규약이다.
- 반드시 지켜야 하는 규약은 아니지만 일부 컬렉션 원소의 비교가 compareTo를 사용해 꼭 명시해야 한다고 했다.
1
2
3
4
5
6
7
8
9
10
11
@Test
void duplicateBigDecimalTreeSetTest() {
// given
Set<BigDecimal> bigDecimals = new TreeSet<>(Set.of(new BigDecimal("2.00"), new BigDecimal("2.0")));
// when
int size = bigDecimals.size();
// then
assertThat(size).isEqualTo(1);
}
1
2
3
4
5
6
7
8
9
10
11
@Test
void duplicateBigDecimalHashSetTest() {
// given
Set<BigDecimal> bigDecimals = new HashSet<>(Set.of(new BigDecimal("2.00"), new BigDecimal("2.0")));
// when
int size = bigDecimals.size();
// then
assertThat(size).isEqualTo(2);
}
- compareTo를 사용하는 TreeSet의 경우에는 2.00과 2.0을 같다고 판단했지만, equals와 hashCode를 사용하는 HashSet에서는 경우에는 그렇지 않다는 것을 볼 수 있다.
따라서 이러한 부분을 인지하고 주의해야 할 것이다.
이전 아이템인 라이브러리를 익히고 사용하라와도 관련이 있다고 볼 수 있다.
int / long
정확한 계산을 위한 BigDecimal의 대안으로는 int 혹은 long 타입의 사용이 있다.
단, 다룰 수 있는 값의 크기가 제한되고, 소수점이 필요한 경우 따로 관리해주어야 한다.
(예시로 달러 -> 센트 계산으로 바꾼다면 소수점 대신 정수를 이용한 계산이 가능할 것이다.)
다뤄야 하는 숫자가 9자리 이하라면 int를, 18자리 이하라면 long의 사용을 고려하자.
정리
정확한 결과값이 필요한 경우 float나 double의 사용을 피해야 한다.
부동 소수점 근사치를 이용한 계산을 하기 때문에 오차가 발생할 수 있다.
대안으로는 코딩 시 불편함이나 성능 저하가 관계 없다면 BigDecimal을 그렇지 않다면 int나 long 타입을 사용하도록 하자.
만약 18자리가 넘어가는 수라면 어쩔 수 없이 BigDecimal을 사용해야 한다.