코테 심화(dfs, bfs, 동적계획법, 그리디 등등)

동적 프로그래밍

• 재귀 + 메모이제이션

이미 계산한 부분을 따로 저장하여 중복 계산하지 않도록 하는 방법.

** 재귀가 크게 중복되지 않는데 이러한 방법을 사용하면 오히려 비효율적이기 때문에 확인해야 한다.

dp문제 만날 때

for문을 이용한 Bottom-up 방식, 재귀를 이용한 Top-down 방식이 있다는 것을 명심.

꼭 하나의 반복문으로만 해결되는 것이 아님.

Bottom-up 방식에서 min, max를 자주 이용한다.

생각이 안나면 가능한 작은 수부터 규칙을 써보거나, 큰 수부터 규칙을 써보고 생각해본다.

• ex) 피보나치 수열 (재귀)

mem[] = -1;

public static int fibonacci(int n)
{
	if(n == 0 || n == 1) return n;
	if(mem[n] != -1) return mem[n];
	
	return mem[n] = fibonacci(n-1) + fibonacci(n-2);
}

• ex) N을 제곱수의 개수로 표현하기. (dp[5] = 2^2 + 1^2 (2개) = 2)

int[] dp = new int[N+1]
dp[1] = 1;

for (int i = 1; i <= N; i++} {
	int min = Integer.MAX_VALUE;
	
	for (int j = 2; j * j <= i; j++) {
		int temp = i - (j*j);
		min = Math.min(min, dp[temp]);
	}
	
	dp[i] = min + 1; //temp에서 제곱 수를 빼기때문에 그 제곱수의 개수인 1을 더해줌.
}

return dp[N];

Bottom-up 방식.

그래프

그래프를 나타내려면 정점을 나타낼 수 있어야 하고, 정점들이 어떻게 연결되어 있는지 나타내는 간선 정보를 표현할 수 있어야 한다.

1. 인접행렬
2. 인접리스트

• 인접행렬은 2차원배열을 통해 그래프를 나타낸 것으로 간선 정보에 따라 원소만 넣으면 되기때문에 구현이 쉽다. 하지만 정점 개수가 너무 많으면 2차원배열 할당자체가 힘들수있고, 한 정점과 연결된 정점을 찾으려면 2차원 배열에서 하나의 열을 모두 순회해야한다는 단점이 있다.

• 인접리스트는 정점이 연결된 정점들을 리스트로 표현하는 방식이다. 이 방식은 원소가 리스트인 1차원 배열로 그래프를 표현가능하다. 메모리가 훨씬 적다는 장점이 있고, 특정 정점과 간선으로 연결된 정점들만 쉽게 순회가능하다. 하지만 임의의 두 정점 사이에 간선이 있는지 알려면 한 정점과 연결된 모든 정점을 순회하며 찾아보아야 하는 단점이 있다.

int[][] result = [[4,3], [4,2], [3,2], [1,2], [2,5]];
//{4,3} 이라면 4가 3보다 우위에 있다는 뜻이라고 가정.

boolean[][] graph = new boolean[result.length][result.length];
//우위에 있다는 것을 true로 표현하는 그래프

for(int[] edge : result)
{
	int u = edge[0] - 1; // -1은 result 값이 1~5이기 때문.
	int v = edge[1] - 1;

	graph[u][v] = true;
}

//이렇게 했을 때 그래프에는 행을 기준으로 열의 index에게 
우위에 있을 때 true 값을 담게 된다.

이진트리

• 이진트리의 순회

1. 전위순회
2. 중위순회
3. 후위순회

전위순회는

노드 -> 왼쪽 서브트리 -> 오른쪽 서브트리 순으로 순회를 진행한다.

중위 순회는

왼쪽 서브트리 -> 노드 -> 오른쪽 서브트리

후위 순회는 양쪽 서브트리를 모두 방문한 후 노드를 방문하는 순회 방식

//전위순회
void pre(Node node){
	if(node == null) return;
	
	System.out.println(node.data);

	pre(node.left);
	pre(node.right);
}

//중위 순회
void in(Node node){
	if(node == null) return;

	in(node.left);

	System.out.println(node.data);

	in(node.right);
}

//후위 순회
void post(Node node){
	if(node == null) return;
	
	post(node.left);
	post(node.right);

	System.out.println(node.data);
}

우선순위 큐

우선순위 큐 = 힙 = ‘최솟값’ 또는 ‘최댓값’을 ‘빠르게’ 찾아내기 위한 ‘완전이진트리’ 형태로 만들어진 자료 구조.

특정 원소 중에서 최대 우선순위를 가지는 값을 효율적으로 구하려고 고안된 자료 구조.

우선순위 큐는 원소의 삽입, 최대 우선 순위 값 뽑기의 두 가지 연산을 지원한다.

PriorityQueue<Integer> pq = new PriorityQueue<>();
PriorityQueue<Integer> pq_2 = new PriorityQueue<>((a,b) -> b-a);
PriorityQueue<Point> pq_3 = new PriorityQueue<>((a,b) -> a.x - b.x);
//pq_3 처럼 Point 같은 클래스를 pq에 담는다면 우선순위 조건을 지정해줄 수 있다.

pq.add(4);
pq.add(2);
pq.add(6);

pq.poll(); // 2
pq.poll(); // 4
pq.poll(); // 6
//pq_2 에서처럼 람다식을 이용해 우선순위가 내림차순 순으로 주어지게 할 수 있다.

투 포인터

특정 조건을 만족하는 연속된 구간을 찾을 때 유용하다.

구간의 시작과 끝을 가리키는 두 포인터를 하나씩 이동시켜가며 구간을 찾게 된다.

int start = 0;
int end = arr.length - 1;

int s = 0;
int e = s;

while(s < arr.length)
{
	if(조건 달성)
	{
		if(e - s < end - start)
		{
			start = s;
			end = e;
		}
		
		(기존 s에 해당되는 것을 지운 뒤 조건 체크하도록)
		s++;
		// s++을 하게되면 (조건을 만족했다는 가정하에) 
		범위가 줄어들고 e++를 하게되면 범위가 줄어든다.
	}
	else if(e < arr.length - 1)
	{
		e++;
		(e++에 해당되는 것을 삽입해서 조건 체크하도록)
	}
}

유니온 파인드

유니온 파인드는 서로소 집합(disjoint set) 자료 구조를 사용하는 알고리즘이다.

서로소 집합은 공통된 원소를 가지고 있지 않은 2개 이상의 집합으로, 유니온 파인드에서는 모든 원소가 자신만 들어 있는 집합에 속한 상태로 시작한다. 이후 원소들이 서로 연결되는 등 정보를 이용하여 집합이 점점 합쳐진다.

즉 서로 연결되어 있는지를 확인할 때 활용가능하다.

//원소들의 연결을 Node라고 했을 때, Node가 일렬로 합쳐지지 않게 하는 방법으로 아래와 같이 사용가능하다.

//루트 노드를 구할 때 부모 노드를 루트 노드로 업데이트하는 방법이다.
//루트 노드를 제외한 연결된 모든 노드의 부모노드가 루트노드가 되기 때문에 O(1)만에 같은 집합에 속하는지 알 수 있다.
//따라서 루트노드가 서로 같다면 같은 집합에 속하게 되는 것이다.

private static class Node{
	private Node parent = null;
	
	public boolean isConnected(Node o){
		return root() == o.root();
	}
	
	public void merge(Node o){
		if(isConnected(o)) return;
		o.root().parent = this;
	}

	private Node root(){
		if(parent == null) return this; // 루트노드 전용
		return parent = parent.root();
	}
}

크루스칼 알고리즘(+유니온 파인드)

• 최소신장트리

  간선에 가중치가 있는 그래프에서 간선의 가중치 합이 최소가 되는 트리

‘간선을 가중치 순으로 정렬한 후 순서대로 순회’하면서 연결되지 않은 두 정점을 잇는 간선을 채택해나가면 된다. 이 방식이 크루스칼 알고리즘이다.

두 정점이 연결되었는지 검사하기 위해 유니온 파인드를 활용한다.

-크루스칼 알고리즘 + 유니온파인드의 활용

int[][] costs = [[0,1,1], [0,2,2], [1,2,5], [1,3,1], [2,3,8]];
//0과 1이 가중치 1인 간선으로 연결되어 있다는 뜻.

class Edge
{
	public final int u;
	public final int v;
	public final int cost;

	private Edge(int u, int v, int cost)
	{
		this.u = u;
		this.v = v;
		this.cost = cost;
	}
}

Edge[] edges = new Edge(costs);
Arrays.sort(edges, (a,b) -> a.cost - b.cost);
//크루스칼 알고리즘을 이용하기 위해 비용이 작은 간선부터 순회

for(Edge edge : edges)
{
	Node node1 = nodes[edge.u];
	Node node2 = nodes[edge.v];
	
	//유니온파인드(연결되어있지 않다면 하나의 집합으로)
	if(node1.isConnected(node2)) continue;
	node1.merge(node2);
	
	totalCost += edge.cost;
}

System.out.print(totalCost);
//cost가 최소로 모두 연결되었을 때의 totalCost.

dfs

완전탐색. 스택과 재귀로 구현이 가능한데 보통 재귀를 선호한다.

for문을 통해 전체를 탐색한다.

visit[]로 방문했는지 체크하고

select[]로 선택한 원소들을 저장한다. 이후 다음 원소를 선택하기 위해 재귀를 통해 전이.

최종 index에 도달했을 때 규칙을 통해 적합한지 검사한다.

최종 index에 전이되고 적합한지 검사한 후 visit[]와 selec을 초기화하고 첫 for문의 i++이 되면 2로 시작하는 모든 경우의 수를 돈다.

//1,2,3,4,5,6,7,8이 있으면 1로 시작하는 모든 경우의 수를 돌게 된 것

탐색 공간의 깊이가 제한되어 있지 않은 문제에서는 적용하기 힘들다.

최단경로를 찾을 수 없다.

• 스택을 이용한 dfs의 템플릿

boolean[] isVisited = new boolean[N];

Stack<Integer> stack = new Stack<>();

//초기 상태
stack.add(/* initialState = */ = 0);

//탐색 진행
while(!stack.isEmpty())
{
	int state = stack.pop();
	
	//중복검사
	if(isVisited[state]) continue;
	isVisited[state] = true;

	//현재 상태 처리
	
	//전이 상태 생성
	for(int next : getNextStates(state))
	{
		if(범위검사){
			범위 벗어나면 제외
			continue;
		}
		
		if(유효성검사){
			문제의 조건 벗어나면 제외
			continue;
		}
	}

	//상태 전이
	stack.push(next);
}

bfs

탐색 상태와 초기 상태 사이의 거리에 따라 주어진 탐색 공간을 탐색한다.

즉, 초기 상태에서 가까운 상태부터 탐색한다. 따라서 목표 상태를 발견했다면 해당 상태가 탐색 공간에 있는 여러 목표 상태 중 최단 경로에 있는 목표 상태라는 것을 알 수 있다.

대부분 DFS의 코드와 동일하다. 하지만 중복 검사의 시점이 다르다.

• 큐를 이용한 bfs 템플릿

boolean[] isVisited = new boolean[N];

Queue<Integer> queue = new LinkedList<>();

queue.add(/* initialState */ = 0);
isVisited[/* initialState */] = true;

while(!queue.isEmpty())
{
	int state = queue.poll();

	/* 현재 상태 state 처리*/

	for(int next : getNextStates(state))
	{
		if(!/*범위 검사 조건*/) continue;
		if(!/*유효성 검사 조건*/) continue;

		//중복검사
		if(isVisited[state]) continue;

		//방문 처
		isVisited[state] = true;
		queue.add(next);
	}
}

백트래킹

dfs, bfs로 구현할 수 있으며 재귀함수 호출 후 다시 방문처리를 false로 해주어 되돌아갈 수 있게하는 방식.

public static void dfs(int depth, int N, int M, int[] numArr)
{
	if(depth == M)
	{
		for(int i : numArr)
		{
			sb.append(i).append(" ");
		}
	}
	
	for(int i = 0; i < N; i++)
	{
		if(isVisited[i]) continue;

		numArr[depth] = i+1;
		isVisited[i] = true;
		dfs(depth + 1, N, M, numArr);
		isVisited[i] = false; // 핵심.
	}
}

다익스트라 알고리즘

하나의 시작 정점으로부터 모든 다른 정점까지의 음의 가중치가 없을 때 최단 경로를 찾는 알고리즘

dist변수를 사용해 최단거리를 기록해가며 조건을 걸어 기록을 갱신한다.

BFS와 비슷하지만 시작 정점부터 다른 정점까지 기록된 거리가 짧은 순서로 방문해야하기 때문에 우선순위 큐를 사용하게 된다.

벨만-포드 알고리즘

BFS, 다익스트라와 같지만 가중치에 음수가 있을 때 사용하는 방법이다.

dist는 출발지로부터 최단거리를 기록하는 1차원 배열이다. 출발지는 0, 나머지는 INF로 초기화한다.

다익스트라처럼 최단거리가 있는 경우 갱신하는 구조까지는 똑같지만 다시한번 for문을 순회하며 음수사이클이 있는지를 확인하는 것이 핵심이다.

최단거리를 정점의 개수 - 1번 돌면서 갱신하고 다시 시도했을때 또 초기화가 일어나면 음수 사이클이 발생한 것을 의미한다.

왜 정점의 개수 - 1번 만큼 노선들을 순회하느냐

예를 들어 1번만 순회했을 때 1번에서 2번까지 가는데 2의 시간이 걸렸다고 가정해보자. 하지만 3에서 1을 가는데 -2의 시간이 걸렸고, 1-2-3-1-2 순서로 방문했을 때 오히려 2번까지 가는 시간이 0으로 단축이 된다.

이런 부분을 체크하기 위해 전체를 반복해서 노드의 개수 -1 만큼 순회하는 것이다.

private static boolean bellmanFord(){  
	time[1] = 0; //시작점임을 체크. (INF가 아니어야 순회할 수 있음.)
  
	for(int i = 1; i < N; i++){ // 노드의 개수 - 1 만큼 갱신.
		for(int j = 0; j < M; j++){  
			Bus bus = busArr[j];  
  
			//출발지는 0으로 갱신해놨기 때문에 INF가 아니라 출발지로부터 이어지는 점들은 순회 가능.
			if(time[bus.start] != INF && time[bus.end] > time[bus.start] + bus.weight){  
				time[bus.end] = time[bus.start] + bus.weight;  
			}  
		}  
	}  
  
	//음수 사이클 확인 (한번 더 돌렸을 때 음수가 되면 계속해서 최단거리가 음수로 갱신되는 음수사이클 존재)
	for(int i = 0; i < M; i++){  
		Bus bus = busArr[i];  
  
		if(time[bus.start] != INF && time[bus.end] > time[bus.start] + bus.weight){  
			return false;  
		}  
	}  
	return true;  
}

플로이드 와샬

음수 사이클이 없는 그래프 내의 각 모든 정점에서 각 모든 정점까지의 최단거리를 모두 구할 수 있는 알고리즘이다. 다익스트라 알고리즘과는 다르게 그래프에 음수 사이클만 존재하지 않으면, 음의 가중치를 갖는 간선이 존재해도 상관이 없다.

for(int i = 0; i < M; i++){  
	st = new StringTokenizer(br.readLine());
	  
	int u = Integer.parseInt(st.nextToken());  
	int v = Integer.parseInt(st.nextToken());  
	int c = Integer.parseInt(st.nextToken());  
  
	// 출발 도시와 도착 도시가 같지만 cost가 다른 경우 1 4 1과 1 4 2가 들어왔을 때 1 4 1을 선택해야 함.  
	arr[u][v] = Math.min(arr[u][v], c);  
}  
  
//플로이드 워셜  
for(int k = 1; k <= N; k++){//경유지  
	for(int i = 1; i <= N; i++){//출발지  
		for(int j = 1; j <= N; j++){//도착지  
			if(arr[i][j] > arr[i][k] + arr[k][j]){  
				arr[i][j] = arr[i][k] + arr[k][j];  
			}  
		}  
	}  
}

그리디 알고리즘

dfs, bfs와 달리 모든 경우의 수를 살펴보지 않고도 최적의 해를 구할 수 있는 알고리즘이다.

그리디 알고리즘에서는 하나의 상태에서 다른 상태로 전이할 때 가장 정답에 근접해지는 단 하나의 상태로만 전이한다.

하지만 현재 상태에서 최선의 상태로 전이를 하는 경우가 독이 될 때가 있는데 이를 잘 판단해 그리디 알고리즘을 적용할 지 선택해야 한다.

트라이

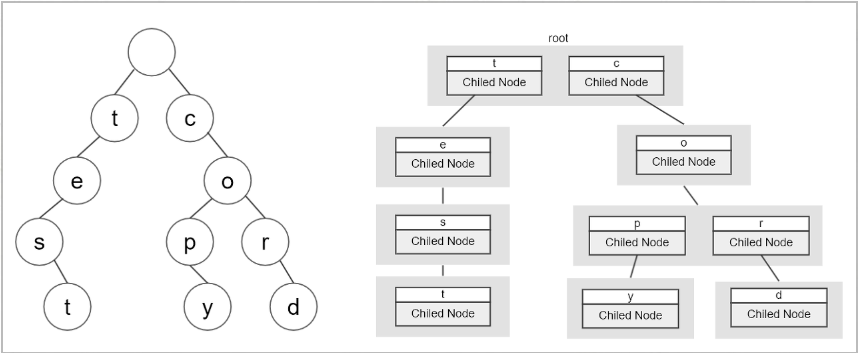
트라이는 트리의 일종으로, 문자열을 다루는 자료 구조이다.

각 노드는 문자 하나와 문자열 완성여부를 나타내며 트라이를 어떤 경로로 타고 내려가는지에 따라 문자열이 조합된다.

기준이 되는 단어들을 왼쪽의 트라이로 만든다. 루트노드는 비어있고 첫 번째 자식노드부터 문자열의 첫 알파벳이 저장된다. 단어의 한 알파벳씩 비교해가며 검색을 진행한다.

static class Node{  
	Map<Character, Node> childNode = new HashMap<>();  
	//자식노드  
	boolean endOfword; // 단어의 끝인지 체크  
}  
  
static class Trie{  
	Node rootNode = new Node(); //루트  
  
	//Trie에 단어 저장.  
	public void insert(String str){  
		Node node = this.rootNode;  
  
		//문자열의 각 알파벳이 자식노드중에 있는지 체크.  
		//없으면 자식노드 새로 생성.  
		for(int i = 0; i < str.length(); i++){  
			//str.charAt(i)라는 키가 바로 붙어있는 자식노드에 없다면,  
			//해당 str.charAt(i)의 key에 해당하는 value는 new Node()이다.  
			//node는 그 노드로 갱신이 된다.  
			node = node.childNode.computeIfAbsent(str.charAt(i), key -> new Node());  
		}  
  
		//저장할 단어의 마지막 알파벳에 매핑되는 노드에 단어의 끝임을 알림.  
		node.endOfword = true;  
	}  
  
	//Trie에서 단어 검색  
	boolean search(String str){  
		Node node = this.rootNode;  
  
		//단어의 각 알파벳마다 노드가 존재하는지 체크.  
		for(int i = 0; i < str.length(); i++){  
			//루트노드의 자식노드에 알파벳이 매핑된 노드가 있다면 노드를 그 자식노드로 갱신 없다면 null
			//이렇게 함으로써 매핑이 됐을 때 자식노드로 타고 내려가는 구조가 됨.  
			node = node.childNode.getOrDefault(str.charAt(i), null);  
  
			if(node == null){  
				return false;  
			}  
		}  
  
		//이 부분은 문제에 따라 바뀔 수 있을 듯.  
		return node.endOfword;  
	}  
}

분할정복

1. 재귀에 대한 이해
2. 탐색에 대한 이해

를 바탕으로

1. 현재 상태의 문제를 풀 수 없는 경우 문제를 분할할 수 있는지 확인
2. 문제를 분할하여 각각 풀이
3. 풀린 문제들을 합침

의 흐름으로 문제를 해결하게 된다.

위상정렬

그래프 알고리즘의 하나이다.

선후관계가 정의된 그래프 구조에서 정렬을 하기 위해 사용한다.

위상 정렬을 사용하기 위해서는 그래프가 순환하면 안된다.

해당 지점과 직전에 해야할 것들의 개수를 저장하는 before_cnt[]를 선언하고

before_cnt[해당지점] = 0인 지점을 queue에 넣는다.

queue.poll() 하고 해당 지점에 연결된 다음 지점들을 순회하면서 조건을 해결해나가면 된다. 다음 지점을 순회할 때 before_cnt[다음지점]–;를 해주면서 선수조건의 개수를 줄여준다. before_cnt[다음지점]이 0이되면 모든 선수조건을 해결했다는 뜻이므로 다음지점도 queue에 넣는다.

최소 스패닝 트리

최소 신장 트리.

크루스칼 알고리즘과 유니온 파인드로 해결할 수 있다.

‘간선을 가중치 순으로 정렬한 후 순서대로 순회’하면서 연결되지 않은 두 정점을 잇는 간선을 채택해나가면 된다.

N개의 노드가 있다면 N-1개의 간선만 채택해야 한다.

가중치가 최소인 간선들을 채택해나가면서 그 간선에 연결되어있는 노드들이 이미 연결되어있는지, 그렇지 않다면 연결시키는 방법으로 구현한다.

자료구조(스택, 큐, 덱)

덱으로는 배열의 원소를 원형으로 돌릴때나 뒤집을 때 for문을 활용하면 용이.

스택은 우선순위를 부여할 때 용이. 이중 for문으로 체크하면 쉬운데 크기가 너무 커서 불가능한 경우 스택을 활용해봐도 좋음.

큐도 마찬가지로 이중 for문으로 체크하면 쉬운데 크기가 너무 커서 불가능한 경우 활용해봐도 좋음. 스택과의 차이는 문제 조건에서 보임. 큐와 스택 모두 무조건 값을 넣는 것이 아닌 index를 넣어 판단하는 것도 있다는 것을 생각.

자료구조 2(우선순위 큐, Map, Set)

단순히 우선순위큐로 값들을 정렬하면서 저장하면 최댓값이나 최솟값 둘 중 하나에만 접근이 가능하다.

이럴때 TreeSet, TreeMap을 활용하면 정렬하면서 저장하는 부분은 같지만 비교적 자유롭게 최소, 최댓값에 접근이 가능하다.